Are the rest of you feeling the end of the semester like I am?  It’s so close!  All this grading has given me a chance to think about my next topic… and I could write about a million different things… But I think I want to continue with simplifying radicals, the natural segue from my last post on Factor Cakes & Ladders.  There’s a chance that some of you out there haven’t quite reached simplifying radicals in your Algebra 1 curriculum this year, so I’ll give it a shot.

Before we begin, let’s lay the groundwork with a few key division vocab words, especially if you’re like me and you do mental gymnastics any time you come across words you don’t use regularly:

• Dividend:  The number “inside the house” when you’re dividing
• Divisor:  The number that’s dividing, or breaking up, the other number
• Quotient:  The answer that results from dividing two numbers.

And pictorially (since, really, I’m a much more visual person…):

Now for Simplifying Radicals:

Simplifying radicals is SO easy… for kids who have mastered their multiplication facts and perfect squares, and who have a great sense of integer division.  In the traditional way of doing things:

• Yes, you can have students memorize their perfect squares and cubes (In fact, maybe you should!  I have been known to quiz my classes on the “list”, at times with a calculator and at times without.  It really depends on the circumstances – the class, the individual ability levels, etc.  We then have a conversation when those perfect squares and cubes come up in our answer and the radical completely disappears.)
• Students then divide their integers until they figure out which perfect square or cube divides the original number nicely.
• They write the root of the perfect square/cube in front (the divisor), and the root of the quotient last, simplifying the first root if they haven’t already.

This takes a whole lot of trial and error for those who struggle with basic math facts.  It’s possible, but I’ve found a much better method that work every single time.  If you’ve read my entry on Solving Equations *the river method*, have you noticed that I tend to prefer the methods that ALWAYS WORK?  Especially for my struggling students?

Let’s dive right in to the most complicated type of example!  The same basic rules apply when you’re working with easier radicals. 

(1)  Create a Factor Ladder/Cake to list all prime factors of 540:   I generally default to ladders because they allow me to work down the page.

(2)  Circle or draw arrows next to the pairs of factors.  In this case, there’s a pair of 2s and a pair of 3s, leaving behind a 3 and a 5.  My key catch phrase here is:  Couples go out on dates, singles stay home.* 

*Yes, I’m probably a terrible teacher for ingraining this “fact” in my students’ minds!  But… I deal with high schoolers.  It helps them to remember, and they mostly find it funny.  Or corny.  Anyway, I spend time talking about that one couple they know that’s ALWAYS together.  YOU know, you could practically morph their names into one, like Ginny + Ronaldo = Ginaldo.  Therefore, you write only ONE 2 and ONE 3 out front of the radical, because they’re each one couple.

**Just wait.  IT GETS WORSE!  I then tell my high school students that couples go out and multiply, and so do singles who stay home. (gasp!)   The singles call one another up and hang out together at the same house.   And if there’s a “couple that’s already out” (here, the -7), it multiplies with the other couples.  The students that pick up on the innuendo find it even more hilarious than the whole dating scenario.  I recommend knowing your audience before you dive right in to these jokes, but I’m telling you, they work as far as memory tricks are concerned.  😀

***Another more PG-friendly version of this is to say “your parents won’t let you out of the house unless you go with a friend – stick together!”  etc, etc.  This also works really well when you start working with cube roots.

(3)  Write out the variable factors: 

Here, we have 2 xs and 5 ys.  To be consistent with my factor ladders, I write the factors vertically, although technically kids can write out the xs and ys however they’d like.

 

(4)  Pair up the variables:  I ask “how many pairs of x do we have?”  One.  So one x goes out front, with none remaining “at home.”  “How many pairs of ys do we have?”  Two.  So two ys, or y squared, are in front of the radical, with one y left “in the house.”

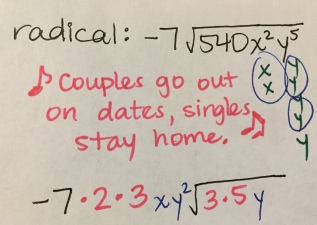
(5)  Simplify!  Multiply the inside of the square root, and multiply the coefficient of the square root.  And voila!  You’re done.

(6)  If the question happens to have all perfect squares (or all perfect cubes), like √(144a²), we talk about how all factors are paired up, so everyone can “leave the house.”  Therefore, there’s no longer a need for our square root sign.  The answer is just 12a.

 

You might ask…

How does this differ from simplifying cube roots??

It doesn’t.  Well, it does, but only slightly.  In this case, students should be looking for groups of 3 instead of pairs.  The students’ parents are only letting them out of the house to go to the mall in groups of 3 this time.

Since there’s one group of 3 and one group of ys, we write one 3 and one y in front of the cube root.  Everything else is stuck “at home.”  Emphasize the point that students MUST write the 3 on the “house” so we know their parents’ rules.  Then they can simplify.

Resources:

You can find a power point I created a while ago, along with the guided notes for FREE(!), on Teachers Pay Teachers.  It’ll give you a sense of how I do my guided notes – I leave blanks so students can’t rush ahead and make silly mistakes.

• This lesson usually takes 1.5 blocks
  • 1st block:  #1 – 18
  • 2nd half:  #19 – 27
  • Some *we do* questions, some *you do* questions
• This is the first time most of my students have seen the ladder method of prime factoring.  *If yours have worked with it before, You shouldn’t need to focus on the first half of the lesson as much.*
• I photocopy pages 1 & 2 front to back
• I make HALF the copies of pages 3 & 4 front to back, and then cut those pages in half.  This is intended to save paper.

You don’t have to use the notes “as is,” but they give you a good starting point.

 

Happy Simplifying!

 

– Ms. Elsie